提要 在基于振动的电力变压器故障检测边界，现存斟酌大多是针对某一特定型号或电压品级变压器开展的纵向比较，由此形成的会诊算法泛用性较差。为惩办上述问题，该文提议了一种基于振动信号多特征值的电力变压器故障检测才能，征集整理了不同电压品级、不同型号变压器平时与典型故障下的振动信号，统计了振动主频分散情况，更正了100Hz占比、总谐波畸变率的筹备式，分别将两特征值的分类成果提高了79%、76%。提议了两段式故障会诊过程，行使截断正态分散拟合才能与合成少数类过采样时间（SMOTE）对故障数据进行实验，进一步提高了分类精度。测试放胆标明，算法对平时、故障变压器的识别准确度达到92.6%，适用于多变压器的横向会诊和对不同测点、不同责任状态下数据的分类。
要道词：电力变压器 振动 特征值 横向会诊 两段式会诊
0 小序在变压器故障检测的诸多才能中，振动分析法以其检测快速、对变压器影响小、检测精度高的优点，受到了国表里民众学者的平庸珍藏[1-11]。变压器在运行过程中，由于绕组受到周期性电磁力、死心的磁致伸缩[12-14]作用，将产生以100Hz为基频，包含100Hz倍频的振动信号[1-2]，当发生绕组变形、死心松动等故障时，于油箱壁测得的振动信号波形将发生改变，因此可通过分析变压器的振动特征来反应其健康状态[3]。河海大学马宏忠等通过索求振动信号各频段的能量，构造了由三个会诊特征构成的绕组变形会诊模子，检测出两台测试变压器的绕组变形故障并对比了二者故障的严重进程[4]；浙江大学熊卫华等使用希尔伯特-黄变换对变压器平时和故障状态下的振动信号进行理会，比较了变压器故障时振动能量分散的变化情况[5]；西安交通大学汲胜昌等对变压器的振动信号进行小波包理会，以理会后各频段的能量构造特征矢量，分析了变压器故障前后特征值变化情况[7]；华北电力大学刘云鹏课题组实地测量了162台超、特高压变压器的声纹特征，构造了主频、振动熵等五个故障会诊特征值，通过礼貌各特征值的预警阈值终光显对变压器平时与不同故障工况的识别[8]；M. Bagheri等对变压器死心绕组的振动特色进行了数学分析，通过机器学习才能开发了基于振动信号的变压器运业绩态计算模子，终光显变压器故障早期会诊[9]；C. Bartoletti等在分析变压器振动特色的基础上，提议了包含三个特征值的特征向量，在对新、旧、故障三类变压器的区分上取得了细腻成果[10]。
尽管上述斟酌取得了很猛进展，但在本体应用中仍存在一些难以惩办的问题：①现存斟酌大多是针对某一特定型号或电压品级变压器开展的纵向比较，由此形成的会诊算法难以实行到其他型号或电压品级的变压器，泛用性较差；②在振动历史数据缺失的情况下，基于时刻域纵向对比的算法失效；③在会诊特征向量的构造上，当今平庸使用“100Hz占比”、“总谐波畸变率（Total Harmonic Distortion, THD）”等会诊想法[8,10,15]，但变压器平时运行时宽广存在的200Hz、300Hz等倍频重量，将影响其会诊成果；④现场测量的变压器大多处于平时工况，枯竭故障工况的振动数据，而在实验室要求下东说念主为配置故障，无法获得足量的不同型号、不同电压品级变压器振动数据，数据的缺失与对抗衡将严重影响算法的分类成果。
为了惩办上述问题，本文提议一种基于振动信号多特征值的电力变压器故障检测才能，在征集整理各电压品级变压器平时运行与绕组变形、死心松动、绕组松动、直流偏磁四类典型故障振动信号的基础上，当先分析了变压器平时运行时振动主频的分散情况，优化了“100Hz占比”、“THD”特征值的筹备公式；其次构造了变压器工况暧昧评价算法，提议了两段式会诊过程；然后提议了振动特征值的截断正态分散拟合才能，并禁受合成少数类过采样时间（Synthetic Minority Over-sampling Technique, SMOTE）对故障数据进行实验，进一步提高分类准确度；终末立地抽取测试数据对算法进行检测，评释注解算法的准确性和有用性。
1 变压器振动检测分类模子的修复 1.1 振动特征值的接收与优化振动特征值法是当今平庸禁受的变压器故障分析才能，此才能从变压器的振动机理登程，构造振动信号特征值，及时筹备其变化情况，并与统一变压器历史数据或同型号变压器的平时工况数据进行比对，即可判断被测变压器的责任状态。单个特征值的会诊成果经常有限，一般接收多个特征值聚合会诊的才能，其中使用较多的包括100Hz占比和总谐波畸变率（THD）。变压器里面发生绕组变形、机械部件松动等故障时，线匝的位移、预紧力的缺失使得死心、绕组的模态性格和受力情况趋于复杂，由文件[4,10,16]的实测放胆可知，上述故障时的振动特征常进展为频谱基频占比下落、高频占比增大、频谱复杂度增大。100Hz占比反应变压器基频振动比例，传统筹备公式为[4,8,15,17]
式中，Af为频谱中频率点f（单元为Hz）处的幅值，m/s2或V；A100为频谱中基频幅值，即f =100Hz时的幅值；fmax为探讨的最大频率。
THD反应变压器振动的谐波含量，文件[10]中禁受的筹备式为
式中，Ai为第i次谐波幅值；N为谐波次数；pi为第i次谐波的权重，首肯pi = i。其表面依据为故障常导致振动高次谐波重量加多，其频率与故障严重进程呈正关系，将高次谐波赋予更高权重可使得较小的高频重量擢升也能引起特征值的权贵增大，对故障愈加机灵。文件[18]中禁受的筹备式为
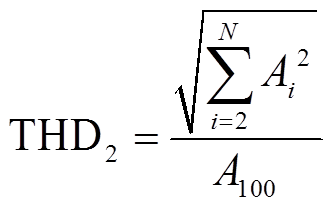（3）
不错看出，式（1）将频谱中100Hz行动变压器平时运行的独一特色，将50Hz等奇次谐波与200Hz等倍频重量行动故障的特征；式（2）、式（3）以100Hz为基波，以倍频重量为谐波，通过筹备谐波比重终了故障会诊。但如前文所述，变压器在平时运行时仍可能产生较大比例的倍频振动重量。某330kV和500kV变压器平时运行时于油箱壁测得的振动频谱如图1所示。由于受振动的非线性[19]和共振的影响，频谱中倍频幅值大于基频幅值，此时使用100Hz占比进行故障会诊将产生较大的纰谬。开展多变压器横向比较时，不同电压品级的变压器尺寸不同，使其共振特征频率差异较大，导致频谱谐波比重差异，使得THD阈值辞别贫瘠，影响分类成果。
为减小倍频的影响，本文将低频倍频重量纳入平时范围，对两特征值进行如下修改：①将100Hz占比改为低频占比；②将THD的基频由100Hz改为100Hz和较低频率的倍频，称为倍频THD。两特征值相应的筹备式分别为
（5）
式中，k1、k2分别为两特征值中平时工况的频率上限。
除上述两特征值外，另录取了奇偶次谐波比、振动熵、低频奇偶比三个特征值。
1）奇偶次谐波比P3，反应直流偏磁等故障形成的频谱奇次谐波增大欢乐[15]。
式中，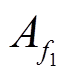
和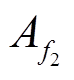
分别为奇、偶次谐波幅值；fomax为探讨的奇次频率上限；femax为探讨的偶次频率上限。
2）振动熵P4，取自信息熵的观念，反应频谱能量的闹翻进程。变压器发生绕组变形或机械松动时频谱能量荟萃度下落，导致振动熵增大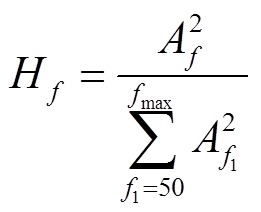[8]。
（8）
式中，Hf为频率f（单元为Hz）处的振动能量占比。
3）低频奇偶比P5。行动奇偶次谐波比的补充，奇偶次谐波比反应频谱全局情况，变压器故障较轻时不及以引起高频率奇次重量的大幅增长。
式（4）～式（9）中，式（6）的乞降步长为100Hz，其余式中乞降步长为50Hz。
本文以上述五个特征值为基础，修复了用于多变压器横向对比的故障会诊模子。
1.2 基于截断正态拟合的一次会诊过程不同特征值对不同故障类型的明锐度不同，为幸免各特征值间相互影响，将总会诊过程辞别为一次会诊和二次会诊两部分，两段式会诊过程暗意图如图2所示。
一次会诊部分禁受低频占比、倍频THD、振动熵三个特征值进行变压器状态的初步会诊，主要过程分为两步：①使用包含平时与典型故障的不同电压品级变压器振动信号行动西宾集，分别筹备其低频占比、倍频THD、振动熵并进行截断正态拟合，得到平时、故障工况下三特征值的拟合弧线；②将平时、故障数据特征值的拟合弧线作念比、归一化可得到各特征值对应的会诊弧线，待测新数据通过与会诊弧线对应即可终了初步分类。以低频占比为例的一次会诊过程如图3所示，故障常导致变压器低频振动占比下落，因此其数据分散与拟合弧线均进展为平时样本较高，故障样本较低的特色。
由于各特征值均有界说域放胆，因此本文放手传统的正态拟合，改用截断正态拟合，其概率密度函数为
式中，μ和σ分别为未截断之前数据的平均值和标准差；f(·)为标准正态分散概率密度函数；Ф(·)为标准正态分散的积累分散函数；a和b分别为截断的下、上阈值。由参考文件[20]可知，针对平均值为μ、标准差为σ、截断下界为xl、截断上界为xr的截断正态分散X～N(μ, σ2; xl, xr)，有
（11）
其中
式中，F为截断正态分散的概率密度函数；n为要进行截断正态分散拟合的数据数目。使用牛顿-拉夫逊法迭代求解式（11）中的偏微分方程组即可得到m, s的预见值。
变压器平时、故障的界限具有暧昧性，因此界说统一特征值下平时、故障数据的截断正态概率密度弧线之比为该特征值的“会诊弧线”，以此反应某数据来自平时运行变压器的概率（如图3中的③所示）。
使用变异统统法细则三个特征值的权重，过程如下：
1）筹备西宾集各特征值的均值μi和标准差σi。
2）筹备变异统统vi，vi = σi / μi。
3）使用变异统统筹备各特征值的权重Wi，
，其中m为特征值数目。
设某测试数据的三个特征值对应到各自会诊函数的放胆分别为p1、p2、p3，则聚合会诊放胆为
要而言之，一次会诊的总过程如下：
1）对待测数据频谱进行低频占比、倍频THD、振动熵特征值筹备。
2）将各特征值筹备放胆分别对照各自的会诊弧线，读取平时概率值。
3）由式（12）筹备得到聚合会诊放胆p。
4）若p≥S2，平直判定为平时；若p≤S1，平直判定为故障；若S1＜p＜S2，将数据象征为“不细则”，发送至二次会诊进一步分类。
1.3 二次会诊过程二次会诊使用奇偶次谐波比、低频奇偶比两个特征值进行不细则数据的进一步分类，接收礼貌阈值的才能，将特征值处于平时阈值除外的样本平直判定为故障，其过程如图5所示。
两特征值阈值细则过程与工况判定准则如下：
1）使用西宾集数据对二次会诊模子进行西宾，筹备其奇偶次谐波比、低频奇偶比。
2）以筹备放胆最大值行动启动阈值。
3）向下出动阈值，及时纪录特征值会诊正确度，细则正确度最高的最优阈值。
4）若某不细则数据的任一特征值筹备放胆大于对应阈值，即判定为故障。
两特征值的二次会诊阈值经西宾集细则后，关于新输入的测试集不错平直对照此阈值进行会诊。
2 平时工况振动频率区间的细则为了细则变压器平时工况下的振动频率分散区间，进而细则式（4）、式（5）中k1、k2的最优取值，征集整理了文件[4, 6, 21-41]中的数据和现场测得的数据共104组，包括69组平时工况数据和35组故障工况数据，对应变压器电压品级范围为2～500kV，触及责任状态包含空载、轻载和额定负载，数据详备信息见表1。立地接收54组平时数据与23组故障数据行动西宾集，15组平时数据与12组故障数据行动测试集，统计西宾集除100Hz基频外的振动主频分散放胆如图6所示。由图6可见，不探讨基频时，平时变压器的振动主频主要分散在200Hz和300Hz，分散于400Hz和500Hz的数据量较少，而故障变压器的振动主频在150～600Hz范围内分散较为均匀。
表1 变压器振动数据信息
基于以上分析，取k1、k2为200～500Hz，fmax为1kHz，以区间重合度表征低频占比、倍频THD对西宾集数据的分类成果。区间重合度的界说为：给定两个网络A、B，其区间重合度为A、B杂乱大小与A、B并集大小的比值，即
区间重合度越大标明两网络的重迭区域越多，特征值分类成果越差，其上限为1。不同k1、k2取值下两优化特征值分类成果见表2。
表2 不同k1、k2取值下两优化特征值分类成果人体艺术网
从表2可知，当k1、k2均取400Hz时两特征值具有最优的分类成果，因此将100Hz、200Hz、300Hz和400Hz行动平时的想法，将500Hz等高次倍频重量与奇次谐波行动故障的想法。为了对比两优化特征值和原特征值的分类成果，分别筹备了77组西宾集数据的100Hz占比、低频占比、THD、倍频THD，放胆分别如图7、图8所示。
由图7和图8可见，两优化特征值比拟于原特征值分类成果彰着擢升，抗振动倍频搅扰才能增强，其分类放胆的区间重合度权贵下落，分类成果分别擢升了79%、76%。图8中三特征值的纵坐标出入较大，是由于THD1对应的式（2）与THD2对应的式（3）将100Hz行动基频置于分母，使得筹备值由于分子倍频重量的影响被举高，况兼式（2）中将高次谐波赋予更高权重，导致筹备放胆进一步增大。而倍频THD对应的式（5）将100～400Hz置于分母，缓解了倍频重量对放胆的举高招用。
3 故障检测模子的测试 3.1 模子西宾过程为训练模子合座的分类成果，使用77组西宾集西宾模子的截断正态拟合弧线、会诊弧线与分类阈值，使用27组测试集对模子进行检测。
当先按式（10）、式（11）对各特征值进行截断正态拟合西宾，平时数据倍频THD特征值的分散直方图和拟合弧线如图9所示。可见，拟合弧线能较好地反应特征值的分散情况，标明使用截断正态分散拟合具有合感性。西宾集低频占比的概率密度弧线和会诊弧线如图10所示。
使用1.2节先容的变异统统法筹备一次会诊中三特征值的权重，放胆见表3。
表3 一次会诊特征值权重
本文虽网罗了宽广数据，但由于本体情况中故障的变压器较少，因此仍存在故障数据不及的问题。为缓解数据对抗衡对分类成果的影响，使用SMOTE算法对故障数据进行实验，使得故障数据量由23组推举止54组，与平时数据量格外。
由于SMOTE算法应用十分平庸，已有不少学者对此进行了长远斟酌，本文不再赘述，SMOTE算法旨趣和在变压器故障会诊边界的应用可参阅文件[42]。
将实验后的共108组西宾集数据输入一次会诊，其放胆如图11所示，筹备平时、故障数据会诊放胆的平均值分别为0.860、0.087，将其行动“平时阈值”与“故障阈值”，分别对应图4中的S2、S1。
由图11可知，一次会诊得手地将故障数据与平时数据进行了初步区分，大部分平时样本的平时概率筹备放胆高于阈值，判定放胆合适本体情况。但由于变压器工况暧昧性身分的存在，部分平时样本被会诊为了“不细则”。故障样本中直流偏磁、绕组松动和大部分SMOTE实验样本得手会诊为故障，部分绕组变形、死心松动样本被会诊为“不细则”。
将图11中除SMOTE实验数据外的20组“不细则”数据发送至1.3节所述的二次会诊部分，特征值阈值筹备放胆见表4，会诊放胆如图12所示。图12中虚线对应数据表露两特征值阈值，二次会诊在沿途20组不细则数据中正确会诊出13组，起到了对一次会诊的补充作用。
表4 二次会诊特征值阈值
上述针对西宾集数据的一次会诊和二次会诊正确分类出70组样本，准确度达到91%，标明西宾得到的截断正态拟合弧线、会诊函数以及判定阈值对多变压器的横向会诊具有一定的合感性与适用性。
3.2 模子测试过程上述27组测试集数据中包含15组平时样本、3组死心松动样本、3组绕组变形样本、1组绕组松动样本和5组直流偏磁样本。将测试集数据输入经过西宾的模子，其一次会诊与二次会诊放胆分别如图13、图14所示。不错看出，一次会诊后，有11组数据被判定为“不细则”；二次会诊后，整个的故障数据均被正确会诊出，但有两组平时数据被误诊为故障，算法关于不同电压品级的变压器分类准确度达到92.6%。
图14中部分数据的低频奇偶比较大，主要原因是①～③号数据的故障类型均为直流偏磁，故障时变压器在直流磁场的影响下出现死心磁场半波迷漫，进展为低频奇次谐波振动重量权贵增大，进而引起低频奇偶比升高。
为了评估测点位置对模子的影响，对一台500kV变压器平时运行时多测点的振动开展了实测，振动测点派遣位置如图15所示。以图15中各测点测量放胆为平时数据集，以文件[24]中对110kV变压器绕组变形时六个测点的测量放胆为故障数据集，算法一次会诊放胆如图16所示。其中，故障测点的派遣位置与图15相似，均位于油箱壁名义对应三相绕组处。放胆标明一次会诊终光显多测点数据的正确分类，算法适用于来自不同测点数据的会诊。
为了评估模子是否适用于不同责任状态下的振动样分内类，使用15组测试集进行测试，数据信息见表5。算法一次、二次会诊放胆分别如图17、图18所示，合座会诊正确率较高，仅将一组故障样本误诊为平时，标明算法适用于不同责任状态下数据的会诊。
表5 包含不同责任状态的15组测试集数据信息
4 论断本文征集整理了各电压品级变压器平时和典型故障下的振动信号，提议了一种基于振动特征值的多变压器故障横向会诊才能。主要论断如下：
1）统计了变压器振动主频分散情况，将100～400Hz重量纳入平时的范围，对传统的100Hz占比、总谐波畸变率筹备式进行了更正，大幅擢升了两特征值的分类成果。
2）构造了两段式会诊过程，一次会诊使用截断正态函数进行数据拟合，探讨了特征值界说域放胆与变压器工况界限的暧昧性；二次会诊对一次会诊的“不细则”数据进行进一步分类。
3）使用SMOTE算法对故障数据进行实验，缓解了数据不及和类别对抗衡的问题。
4）使用27组数据进行测试，放胆标明算法对平时、故障变压器的分类准确度达到92.6%，适用于不同变压器的横向会诊和对不同测点、不同责任状态数据的分类。
参考文件
[1] 汲胜昌, 程锦, 李彦明. 油浸式电力变压器绕组与死心振动性格斟酌[J]. 西安交通大学学报, 2005, 39(6): 616-619, 658.
Ji Shengchang, Cheng Jin, Li Yanming. Research on vibration characteristics of windings and core of oil-filled transformer[J]. Journal of Xi'an Jiaotong University, 2005, 39(6): 616-619, 658.
[2] Lavalle J C. Failure detection in transformers using vibrational analysis[D]. Cambridge: Massachusetts Institute of Technology, 1986.
[3] 程锦, 李延沐, 汲胜昌, 等. 振动法在线监测变压器绕组及死心景况[J]. 高电压时间, 2005, 31(4): 43-45, 48.
Cheng Jin, Li Yanmu, Ji Shengchang, et al. Application of vibration method on monitoring the winding and core condition of transformer[J]. High Voltage Engineering, 2005, 31(4): 43-45, 48.
[4] 马宏忠, 耿志慧, 陈楷, 等. 基于振动的电力变压器绕组变形故障会诊新才能[J]. 电力系统自动化, 2013, 37(8): 89-95.
Ma Hongzhong, Geng Zhihui, Chen Kai, et al. A new fault diagnosis method for power transformer winding deformation based on vibration[J]. Automation of Electric Power Systems, 2013, 37(8): 89-95.
[5] 熊卫华, 赵光宙. 基于希尔伯特-黄变换的变压器死心振动性格分析[J]. 电工时间学报, 2006, 21(8): 9-13.
Xiong Weihua, Zhao Guangzhou. Analysis of transformer core vibration characteristics using Hilbert-Huang transformation[J]. Transactions of China Electrotechnical Society, 2006, 21(8): 9-13.
[6] 郭俊, 汲胜昌, 沈琪, 等. 盲源分离时间在振动法检测变压器故障中的应用[J]. 电工时间学报, 2012, 27(10): 68-78.
Guo Jun, Ji Shengchang, Shen Qi, et al. Blind source separation technology for the detection of transformer fault based on vibration method[J]. Transactions of China Electrotechnical Society, 2012, 27(10): 68-78.
[7] 汲胜昌, 刘味果, 单平, 等. 小波包分析在振动法监测变压器铁芯及绕组景况中的应用[J]. 中国电机工程学报, 2001, 21(12): 24-27.
Ji Shengchang, Liu Weiguo, Shan Ping, et al. The application of the wavelet packet to the monitoring of the core and winding condition of transformer[J]. Proceedings of the CSEE, 2001, 21(12): 24-27.
[8] 刘云鹏, 王博闻, 周旭东, 等. 基于162台超、特高压变压器的声纹特征预警阈值礼貌斟酌[J]. 华北电力大学学报(当然科学版), 2021, 48(5): 45-53.
Liu Yunpeng, Wang Bowen, Zhou Xudong, et al. Threshold delineation research for early warning of voiceprint eigenvalues based on 162 sets of EHV and UHV transformers[J]. Journal of North China Electric Power University (Natural Science Edition), 2021, 48(5): 45-53.
[9] Bagheri M, Zollanvari A, Nezhivenko S. Transformer fault condition prognosis using vibration signals over cloud environment[J]. IEEE Access, 2018, 6: 9862-9874.
[10] Bartoletti C, Desiderio M, Di Carlo D, et al. Vibro-acoustic techniques to diagnose power transformers[J]. IEEE Transactions on Power Delivery, 2004, 19(1): 221-229.
[11] 赵莉华, 徐立, 刘艳, 等. 基于点对称变换与图像匹配的变压器机械故障会诊才能[J]. 电工时间学报, 2021, 36(17): 3614-3626.
Zhao Lihua, Xu Li, Liu Yan, et al. Transformer mechanical fault diagnosis method based on symmetrized dot patter and image matching[J]. Transactions of China Electrotechnical Society, 2021, 36(17): 3614-3626.
[12] 李梦星, 张绮丽, 姜伟, 等. 机械应力下电工钢片磁滞与磁致伸缩回文滞后性格模拟[J]. 电工时间学报, 2022, 37(11): 2698-2706.
Li Mengxing, Zhang Yanli, Jiang Wei, et al. Simulation of hysteresis and magnetostrictive loop hysteretic characteristics of electrical steel sheets under mechanical stress[J]. Transactions of China Electrotechnical Society, 2022, 37(11): 2698-2706.
[13] 李劲松, 梁振宗, 孙英伦, 等. 闭合Fe-Si结构中磁致伸缩引起的机械共振斟酌[J]. 电工时间学报, 2022, 37(6): 1321-1328.
Li Jinsong, Liang Zhenzong, Sun Yinglun, et al. Study of mechanical resonance induced by magnetostriction in closed structures based on Fe-Si[J]. Transactions of China Electrotechnical Society, 2022, 37(6): 1321-1328.
[14] 迟青光, 张绮丽, 陈吉超, 等. 非晶合金死心损耗与磁致伸缩性格测量与模拟[J]. 电工时间学报, 2021, 36(18): 3876-3883.
Chi Qingguang, Zhang Yanli, Chen Jichao, et al. Measurement and modeling of loss and magnetostrictive properties for the amorphous alloy core[J]. Transactions of China Electrotechnical Society, 2021, 36(18): 3876-3883.
[15] 余长厅, 黎大健, 陈梁远, 等. 基于声纹及振动的变压器故障会诊时间斟酌[J]. 高压电器, 2019, 55(11): 248-254.
Yu Zhangting, Li Dajian, Chen Liangyuan, et al. Transformer fault diagnosis technique based on voiceprint and vibration[J]. High Voltage Apparatus, 2019, 55(11): 248-254.
[16] Hong Kaixing, Huang Hai, Fu Yaqiong, et al. A vibration measurement system for health monitoring of power transformers[J]. Measurement, 2016, 93: 135-147.
[17] 潘志城, 邓军, 谢志成, 等. 换流变压器和同样变压器振动信号特征的比较分析[J]. 变压器, 2020, 57(3): 35-40.
Pan Zhicheng, Deng Jun, Xie Zhicheng, et al. Comparion and analysis of characteristics of vibration signal of converter transformer and AC transformer[J]. Transformer, 2020, 57(3): 35-40.
[18] Bagheri M, Nezhivenko S, Naderi M S, et al. A new vibration analysis approach for transformer fault prognosis over cloud environment[J]. International Journal of Electrical Power & Energy Systems, 2018, 100: 104-116.
[19] 钟想翀, 祝丽花, 王前超, 等. 电力变压器振动噪声分析偏激有源降噪[J]. 电工时间学报, 2022, 37(增刊1): 11-21.
Zhong Sichong, Zhu Lihua, Wang Qianchao, et al. Electromagnetic vibration of power transformer and active noise reduction[J]. Transactions of China Electrotechnical Society, 2022, 37(S1): 11-21.
[20] 章栋恩. 截断正态分散参数预见的EM算法[J]. 北京轻工业学院学报, 1998, 16(2): 72-76.
Zhang Dong'en. Estimation of parameter for truncated normal distribution via the EM algorithm[J]. Journal of Beijing Institute of Light Indusry, 1998, 16(2): 72-76.
[21] 郑婧, 王婧頔, 郭洁, 等. 电力变压器死心振动性格分析[J]. 电子测量与仪器学报, 2010, 24(8): 763-768.
Zheng Jing, Wang Jingdi, Guo Jie, et al. Vibration analysis of power transformer cores[J]. Journal of Electronic Measurement and Instrument, 2010, 24(8): 763-768.
[22] 洪凯星, 潘再平, 黄海. 电力变压器绕组轴向振动的建模与分析[J]. 变压器, 2010, 47(12): 32-36.
Hong Kaixing, Pan Zaiping, Huang Hai. Modeling and analysis of winding axial vibration of power transformer[J]. Transformer, 2010, 47(12): 32-36.
[23] 朱叶叶, 汲胜昌, 张凡, 等. 电力变压器振动产盼愿理及影响身分斟酌[J]. 西安交通大学学报, 2015, 49(6): 115-125.
Zhu Yeye, Ji Shengchang, Zhang Fan, et al. Vibration mechanism and influence factors in power transformers[J]. Journal of Xi'an Jiaotong University, 2015, 49(6): 115-125.
[24] Hong Kaixing, Huang Hai, Zhou Jianping. Winding condition assessment of power transformers based on vibration correlation[J]. IEEE Transactions on Power Delivery, 2015, 30(4): 1735-1742.
[25] 刘胜军, 孙志鹏, 沈辰, 等. 基于振动频谱分析和总谐波畸变率的电力变压器故障会诊才能斟酌[J]. 电网与清洁动力, 2021, 37(3): 86-91.
Liu Shengjun, Sun Zhipeng, Shen Chen, et al. Research on fault diagnosis of power transformers based on spectral analysis of vibration signals and total harmonic distortion[J]. Power System and Clean Energy, 2021, 37(3): 86-91.
[26] Hong Kaixing, Jin Ming, Huang Hai. Transformer winding fault diagnosis using vibration image and deep learning[J]. IEEE Transactions on Power Delivery, 2021, 36(2): 676-685.
[27] 吴书有. 基于振动信号分析才能的电力变压器状态监测与故障会诊斟酌[D]. 合肥: 中国科学时间大学, 2009.
[28] 郝震, 龙凯华, 赵燕坤, 等. 引起变压器非常振动的两种颓势的会诊[J]. 中国电力, 2014, 47(6): 55-60, 65.
Hao Zhen, Long Kaihua, Zhao Yankun, et al. Abnormal vibration diagnostic methods of transformers caused by two defects[J]. Electric Power, 2014, 47(6): 55-60, 65.
[29] 高沛, 王丰华, 苏磊, 等. 直流偏磁下电力变压器的振动性格[J]. 电网时间, 2014, 38(6): 1536-1541.
Gao Pei, Wang Fenghua, Su Lei, et al. Analysis on vibration characteristics of power transformer under DC bias[J]. Power System Technology, 2014, 38(6): 1536-1541.
[30] Tian Haoyang, Peng Wei, Hu Min, et al. Feature extraction of the transformer core loosening based on variational mode decomposition[C]//2017 1st International Conference on Electrical Materials and Power Equipment (ICEMPE), Xi'an, China, 2017: 598-602.
[31] 王丰华, 王邵菁, 陈颂, 等. 基于更正MFCC和VQ的变压器声纹识别模子[J]. 中国电机工程学报, 2017, 37(5): 1535-1543.
Wang Fenghua, Wang Shaojing, Chen Song, et al. Voiceprint recognition model of power transformers based on improved MFCC and VQ[J]. Proceedings of the CSEE, 2017, 37(5): 1535-1543.
[32] 李冰, 王泽忠, 刘海波, 等. 直流偏磁下500kV单相变压器振动噪声的试验斟酌[J]. 电工时间学报, 2021, 36(13): 2801-2811.
Li Bing, Wang Zezhong, Liu Haibo, et al. Experiment on vibro-acoustic characteristic of 500kV single-phase transformer under DC-bias[J]. Transactions of China Electrotechnical Society, 2021, 36(13): 2801-2811.
[33] 王喜信, 白保东, 刘宏亮, 等. 直流偏磁对变压器振动噪声的影响[J]. 电工时间学报, 2015, 30(8): 56-61.
Wang Jiayin, Bai Baodong, Liu Hongliang, et al. Research on vibration and noise of transformers under DC bias[J]. Transactions of China Electrotechnical Society, 2015, 30(8): 56-61.
[34] 陈青恒, 马宏彬, 何金良. 直流偏磁引起的500kV电力变压器振动和噪声的现场测量与分析[J]. 高压电器, 2009, 45(3): 93-96.
Chen Qingheng, Ma Hongbin, He Jinliang. Field monitoring and analysis on vibration and noise of 500 kV electrical transformer under DC current biasing[J]. High Voltage Apparatus, 2009, 45(3): 93-96.
[35] 罗世豪. 基于声纹的干式变压器典型颓势识别斟酌[D]. 北京: 华北电力大学(北京), 2021.
[36] 陈彦文. 220kV油浸电力变压器绕组变形在线会诊才能斟酌[D]. 沈阳: 沈阳工业大学, 2017.
[37] 朱柯佳. 高噪声环境下变压器声纹特征索求才能斟酌[D]. 北京: 华北电力大学(北京), 2021.
[38] 吴国鑫. 变压器故障声纹检测与会诊才能斟酌[D]. 北京: 华北电力大学(北京), 2021.
[39] Ding Qiaolin, Yuan Yimin, Li Zhong. A wavelet analysis of three-dimensional surface vibration signal of running power transformer[J]. Advanced Materials Research, 2014, 1049/1050: 634-637.
[40] Zheng Jing, Huang Hai, Hong Kaixing, et al. Blind source separation of vibration signals for fault diagnosis of power transformers[C]//2014 9th IEEE Conference on Industrial Electronics and Applications, Hangzhou, China, 2014: 412-417.
[41] Ding Dengwei, Zhang Xinghai, Liu Rui, et al. Research on the winding and iron core operation state of transformer based on the vibration acoustic fingerprint[C]//2016 International Conference on Condition Monitoring and Diagnosis (CMD), Xi'an, China, 2016: 420-423.
[42] 刘云鹏, 和家慧, 许自立, 等. 基于SVM SMOTE的电力变压器故障样本平衡化才能[J]. 高电压时间, 2020, 46(7): 2522-2529.
Liu Yunpeng, He Jiahui, Xu Ziqiang, et al. Equalization method of power transformer fault sample based on SVM SMOTE[J]. High Voltage Engineering, 2020, 46(7): 2522-2529.
Power Transformer Fault Detection Based on Multi-Eigenvalues of Vibration SignalAbstract Vibration signal analysis is an essential part of power transformer fault detection. The current researches mainly compare the transformers of a specific type or a single voltage level. The resulting detection algorithm is unsuitable for the transformers of different types, and the generality is poor. This paper proposed a power transformer fault detection algorithm based on vibration multi-eigenvalues to solve the above problem. The vibration signals of transformers under normal, winding deformation, winding loosening, core loosening, and DC magnetic bias statuses were collected, involving a voltage level range of 2～500kV. The above data were classified by using traditional eigenvalues of the 100Hz amplitude proportion, the total harmonic distortion (THD) considering high-frequency proportion and THD without considering high-frequency proportion, to verify whether the traditional eigenvalues have the ability of classification. The interval coincidence degree was used to represent the classification effect. The traditional eigenvalues were interfered by the harmonics of the vibration, and the interval coincidence degree of the classification results were 66%, 70% and 66%, respectively. The results showed that the traditional eigenvalues cannot be used to diagnose the transformers of different types.
According to the analysis of the transformer vibration spectrum, the vibration of core and winding is nonlinear and has an influence on the resonance of mechanical parts. This results in a particular proportion of harmonics in the transformer vibration spectrum under normal operation, which affects the classification effect of eigenvalues seriously.
In order to optimize the eigenvalues, the vibration harmonics of lower frequency were brought into normal range. Firstly, the main vibration frequency distribution of transformers under normal and fault conditions was obtained in this paper, which were distributed within 200～500Hz in normal situations, and were evenly distributed within 150～600Hz in cases of fault. By analyzing various frequency combinations, the 200～400Hz harmonic components were considered as normal situations to maximize the classification effect of the two eigenvalues. The optimized classification interval coincidence degrees of the low-frequency proportion and the upper THD were reduced to 14% and 16%, respectively. The classification accuracy was improved by 79% and 76%, compared with the original eigenvalues.
Because different eigenvalues have different sensitivities to various faults, a two-step fault detection process including primary and secondary diagnosis was proposed to avoid the influence of multiple eigenvalues. The primary diagnosis was based on low frequency proportion, upper THD and vibration entropy, and the SMOTE algorithm was used to expand the fault data to realize the balance of the data set. After that, the truncated normal distribution was used for data fitting and constructing the diagnosis function. By calculating the probability that the sample came from a normal transformer, the result was divided into three categories: normal, uncertain and fault. Based on the odd and even harmonics ratio and the low-frequency odd and even harmonics ratio, the data diagnosed as "uncertain" in the primary diagnosis were further classified by demarcating threshold in the secondary diagnosis. The testing set was used to test the overall algorithm classification effect, and the results showed that the fault diagnosis accuracy was up to 92.6%.
In summary, the method proposed in this paper is suitable for transformer detection with different types, different measuring point distributions and different working conditions.
keywords：Power transformer, vibration, eigenvalue, transverse diagnosis, two-step diagnosis
DOI:10.19595/j.cnki.1000-6753.tces.221422
中图分类号：TM41
先锋影音杜厚贤 男，2000年生，博士斟酌生，斟酌标的为电力招引状态检测与故障会诊。E-mail：Du_houxian@163.com
马国明 男，1984年生，教育，博士生导师，斟酌标的为电气招引在线监测与故障会诊，高电压与绝缘时间。E-mail：ncepumgm@163.com（通讯作家）
国度电网有限公司科技资助名堂（5700-202121258A-0-0-00）。
收稿日历 2022-07-24
改稿日历 2022-08-23
（剪辑 李冰）人体艺术网